KERMIT V2.0
Welcome to the KERMIT code documentation. KERMIT has been introduced in our EMNLP2020 paper, although it has a longer history.
KERMIT aims to collaborate with other Neural Networks (for example, with Transformers) for exploiting structures in decision making and
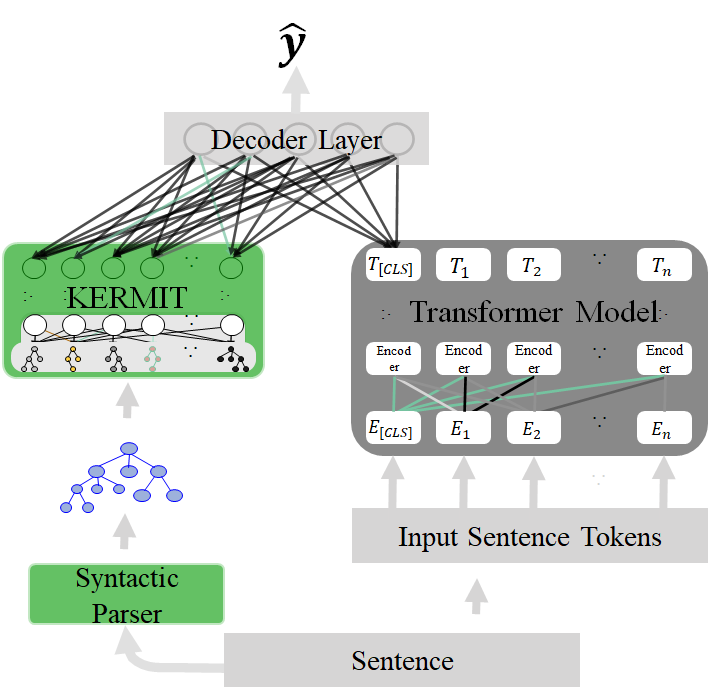
KERMIT architecture
and for explaining how decisions are made using structures:
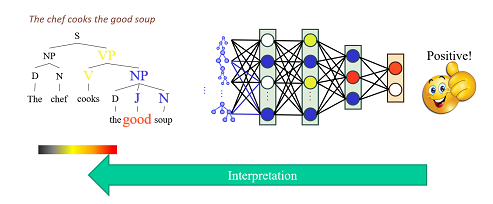
KERMIT Explanation Pass
kerMIT structure encoders
This package contains the Distributed Structure Encoders. These are responsible for taking structured data and producing vectors that are representing these structured data as their substructures in a reduced space (see the following figure).

KERMIT’s Generic Distributed Structure Encoder (or Embedder, what do you prefer?)
Distributed Structure Embedder (DSE)
- class kerMIT.structenc.dse.DSE
Distributed Structure Embedder (DSE): this is the abstract class for all the structure embedders.
Given a structure \(s\), the main aim of a DSE is to produce its embedding \(\vec{s} \in R^d\) in a reduced space \(R^d\) which represents \(s\) by its substrucures. This is obtained by obtaining \(\vec{s} \in R^d\) as a weighted sum of all the substructures \(\sigma\) foreseen in \(S(s)\) according to the specific structure embedder:
(1)\[\vec{s} = \sum_{\sigma \in S(s)} \omega_\sigma W\vec{e}_{\sigma} = \sum_{\sigma \in S(s)} \omega_\sigma \vec{\sigma} = W\sum_{\sigma \in S(s)} \omega_\sigma \vec{e}_{\sigma} = W\vec{e_{s}}\]where \(W\) is the embedding matrix, \(\vec{e}_{\sigma}\) is the one-hot vector of the substructure \(\sigma\) in the space \(R^n\), \(\omega_{\sigma}\) is the scalar weight of the substructure \(\sigma\), \(\vec{\sigma}\) is the vector representing the structure \(\sigma\) in the smaller space \(\vec{\sigma} = W\vec{e}_{\sigma}\in R^d\), and \(\vec{e_{s}} = \sum_{\sigma \in S(s)} \omega_{\sigma}\vec{e_{\sigma}}\) is the vector representing the initial structure \(s\) in the space \(R^n\).
- abstract ds(structure)
given a structure \(s\), produces the embedding \(\vec{s} \in R^d\) (see Equation (1)). This is generally obtained recursively on the components of the structure plus a composing operation.
- Parameters
structure – this is the structure \(s\) that has to be decomposed in substructures.
- Returns
\(\vec{s}\) which is an Array or a Tensor according to the implementation.
- abstract dsf(structure)
given a structure \(\sigma\), it produces the vector \(\vec{\sigma} = W\vec{e}_{\sigma}\in R^d\) representing that single structure in the embedding space \(R^d\) (see Equation (1)). This is generally obtained recursively on the components of the structure plus a composing operation .
- Parameters
structure – this is the structure \(\sigma\) that has to be transformed in a vector representing only that structure.
- Returns
\(\vec{\sigma}\)
- abstract dsf_with_weight(structure)
given a structure \(\sigma\), it produces the vector \(\vec{\sigma}\) representing that single structure in the embedding space \(R^d\) and its weight \(\omega_{\sigma}\) (see Equation (1)).
- Parameters
structure – this is the structure that has to be transformed in a vector representing only that structure.
- Returns
(\(\vec{\sigma}\), \(\omega_{\sigma}\))
Distributed Tree Embedder (DTE)
- class kerMIT.structenc.dte.DTE(LAMBDA=1.0, dimension=4096, operation=<function fast_shuffled_convolution>)
- The Distributed Tree Encoder is applied to trees
and represents trees in the space of subtrees as defined in Duffy&Collins (2001) by means of reduced vectors. It has been firstly implemented in the Distributed Tree Kernels, ICML 2012 Zanzotto&Dell’Arciprete.
Let define trees as the root label \(r\) and the list of its subtrees:
\[\sigma = (r,[t_1,...,t_k])\]where \(t_i\) are trees. Leaves have an empty list of subtrees. Terms of Equation (1) are then the following:
1. \(\vec{\sigma} = \Phi(\sigma) = \begin{cases} \vec{r} & \text{if } \sigma \text{ is a leaf}\\ (\vec{r} \circ (\Phi(t_1) \circ \ldots \circ \Phi(t_n))) & \text{otherwise}\end{cases}\) where \(\vec{r}\) is the vector associated to the label of \(r\) and \(\circ\) is the chosen vector composition operation;
2. \(\omega_\sigma = \sqrt \lambda^n\) where \(\lambda\) is the factor penalizing large subtrees and \(n\) is the number of nodes of the subtree \(\sigma\)
3. \(S(t)\) is the set containing the relevant subtrees of \(t\) where a relevant subtree \(\sigma\) of \(t\) is any subtree rooted in any node of \(t\) with the only constraint that, if a node of is contained in the subtree, all the siblings of this node in the initial tree have to be in the subtree
To keep things simple, terms of Equation (1) are also presented with a running example. Given a tree in the classical parenthetical form:
(NP (DT the) (JJ) (NN ball))\(\vec{\sigma}\) is obtained by transforming node labels in the related vectors and by putting the operation \(\circ\) instead of blanks:
\[\vec{\sigma} = (\vec{NP} \circ (\vec{DT} \circ \vec{the}) \circ (\vec{JJ})\circ (\vec{NN} \circ \vec{ball}))\]This is an example of construction of the \(S(t)\) for a very simple tree (taken from Moschitti’s personal page in Trento):
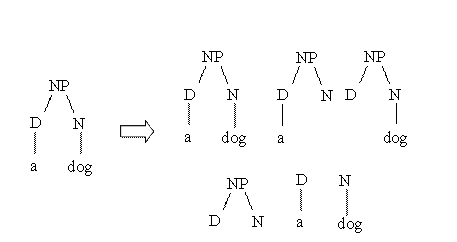
- param LAMBDA
the penalizing factor \(\lambda\) for large subtrees
- param dimension
the dimension \(d\) of the embedding space \(R^d\)
- param operation
the basic operation \(\circ\) for composing two vectors
- ds(tree)
This general method is implemented by dt(tree)
- dsf(tree)
given a structure \(\sigma\), it produces the vector \(\vec{\sigma} = W\vec{e}_{\sigma}\in R^d\) representing that single structure in the embedding space \(R^d\) (see Equation (1)). This is generally obtained recursively on the components of the structure plus a composing operation .
- Parameters
structure – this is the structure \(\sigma\) that has to be transformed in a vector representing only that structure.
- Returns
\(\vec{\sigma}\)
- dsf_with_weight(tree)
given a structure \(\sigma\), it produces the vector \(\vec{\sigma}\) representing that single structure in the embedding space \(R^d\) and its weight \(\omega_{\sigma}\) (see Equation (1)).
- Parameters
structure – this is the structure that has to be transformed in a vector representing only that structure.
- Returns
(\(\vec{\sigma}\), \(\omega_{\sigma}\))
- dt(tree)
takes as input a tree and produces
- Parameters
tree –
- Returns
- dtf_and_weight(tree)
given a tree \(\sigma\) produces the pair \((\vec{\sigma},\omega_\sigma)\):
\(\vec{\sigma} = \Phi(\sigma) = \begin{cases} \vec{r} & \text{if } \sigma \text{ is a leaf}\\ (\vec{r} \circ (\Phi(t_1) \circ \ldots \circ \Phi(t_n))) & \text{otherwise}\end{cases}\) where \(\vec{r}\) is the vector associated to the label of \(r\) and \(\circ\)
\(\omega_\sigma = \sqrt \lambda^n\) where \(\lambda\) is the factor penalizing large subtrees and \(n\) is the number of nodes of the subtree \(\sigma\)
Examples in the general description of the class.
- Parameters
tree – \(\sigma\), which is a Tree
- Returns
\((\vec{\sigma},\omega_\sigma)\), which is a vector (Array or Tensor) and a scalar
- substructures(tree)
it produces all the substructures of \(s\) foreseen according to the specific structure embedder, that is, \(S(s)\) (see Equation (1))
- Parameters
structure – this is the structure where substructure are extracted from.
- Returns
\(S(s)\) as a list
- subtrees(tree)
- Parameters
tree – tree in parienthetic form
- Returns
all subtrees